Why Data Structures?

When I first began solving LeetCode problems, I had very little knowledge of how to leverage data structures when solving algorithms. As a result, there were many problems labeled "Easy" that I simply could not solve. One of these problems was the well-known algorithm Valid Parentheses. In this post I'll highlight my eventual solution to this problem, and how the stack data structure helped me get to it. Example code is written in JavaScript and Ruby.

In the Valid Parentheses problem, you are asked to write an algorithm that accepts a string consisting only of opening and closing brackets ('(', ), '{', '}', '[', ']') and return whether the input string's parentheses are in a valid order. Some examples of valid inputs include '(){}[]', '({})', '{[()()()]}'. Invalid inputs include '{(})', ')(', '[[['.

My first attempt at solving this problem worked in the sense that I was able to return true or false for valid and invalid inputs, respectively. I always solve my algorithms in a REPL, so I was able to test my solution. But when I copied my solution into LeetCode and hit 'submit', I got the dreaded LeetCode Time Limt Exceeded error. I quickly realized this was because my solution relied on a nested for loop, and had a time complexity of a whopping O(n²) while the LeetCode tests expected O(n). Yikes! I needed to find a way to solve this problem with only one iteration of the string. So I started researching DSA topics, and learned about the stack data structure.

What Is A Stack?

A stack is a data structure closely related to Queues and Deques. The name "stack" is an appropriate one. Imagine a stack of paper. There a limited number of tasks one usually performs with a stack of paper. They typically include reading from the page at the top, removing a page from the top, and adding a new page to the top of the stack. Those same tasks are the only tasks one can perform with a stack in code. To represent a stack with an array, all we need to do is limit ourselves to .push(), .pop(), and simply reading the last element of an array. The stack is often referred to as being a 'LIFO' (Last In, First Out) system, because the last element to be added is the only one which can be removed.

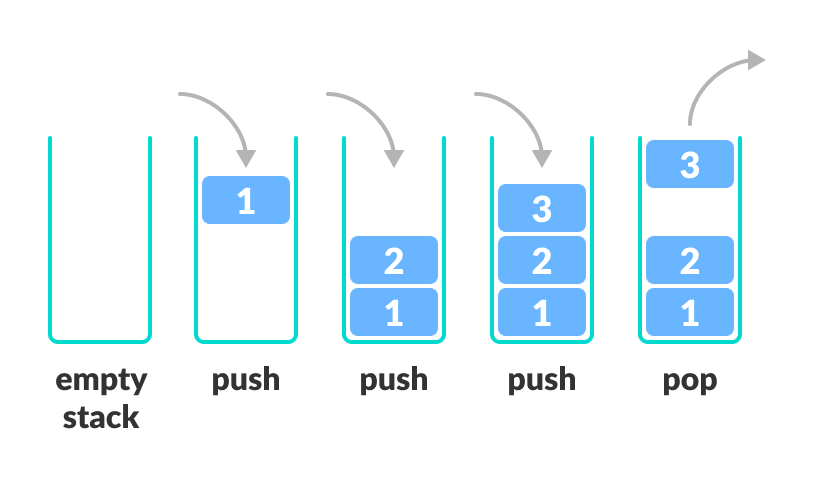
Thinking back to the Valid Parentheses problem, what we ultimately need to keep track of is the order of the parentheses as we iterate. More specifically, whenever we iterate over a closing bracket, we need to check if that bracket is a valid closing bracket for the most recent opening bracket. If we can do that, we can return false if it's not. If we iterate over the whole input string and don't find any invalid closing brackets, the last thing we need to check is whether we have any unclosed opening brackets. A stack lets us do all of that in one pass. The last thing we need is to be able to know whether a given character is a closing bracket or opening bracket, for which we'll use a brackets variable storing the string '{}[]()'.

The Solution

JavaScript:

const isValid = s => {
    const brackets = '{}[]()';
    const stack = [];
    for (const bracket of s) {
        const bracketIdx = brackets.indexOf(bracket);
        if (bracketIdx % 2 === 0) {
            stack.push(bracketIdx + 1);
        } 
        else {
            if (stack.pop() !== bracketIdx) return false;
        }
    }
    return stack.length === 0;
};

console.log(isValid('([]{})'));
// => true

console.log(isValid('([{]})'));
// => false

Ruby:

def is_valid(s)
    brackets = '{}[]()'
    stack = []
    s.each_char do |bracket|
        bracket_idx = brackets.index bracket
        if bracket_idx % 2 == 0
            stack << bracket_idx + 1
        else
            return false if stack.pop != bracket_idx
        end
    end
    stack.size == 0
end

puts is_valid '([]{})'
# => true

puts is_valid '([{]})'
# => false

With this solution, the element in the stack's last index will always be the next valid closing bracket. By using a brackets variable containing the string '{}[]()', we can always deduce whether a given bracket is an opening or closing bracket, using the indexes of the brackets variable. Let's follow the flow with an input of '[])':

1. '[' is an opening bracket, so we store the index 3 at the end of the stack. We use the brackets variable to find the index.
2. ']' is a closing bracket, so we remove the last index of the stack and compare it with the our current bracketIdx. Since they match, we continue.
3. ')' is a closing bracket. We remove the last index from the stack and compare it with the current bracketIdx. Since the stack is was empty, the last element in the stack was actually null, which is not equal to our bracketIdx, we we return false.

By using a stack, I was able to find a solution with a time complexity of O(n), and finally got past LeetCode's Time Limit Exceeded error. The experience of finding a new, unintuitive data structure and leveraging it to craft a solution really opened my eyes to what data structures can offer. Since my experience with Valid Parentheses, my whole approach to solving algorithms has shifted. Instead of going straight to coding when I think of a solution, I try to challenge myself to optimize.

Conclusion

Data structures can stand as powerful tools when writing algorithms. They often do not offer any extra direct functionality. A stack is just an array a programmer treats as having less capability. They do this by only using methods which add, read, or remove the last item of the array. But it's that limitation, or more specifically its implementation, that can come in handy when the order of iterated items matters in an algorithm.